Optimization
손글씨를 디지털 텍스트로 변환하는 문제는 가장 대표적인 머신러닝입니다. 이를 위해서 에러를 정의하고 반복학습을 통해서 모수를 바꿔나감으로써, 정확도를 높여나갑니다. 이처럼 대다수 머신러닝은 모로 가든 “정확하게” 맞추는 게 중요하지, 추정한 모수의 성질 따위는 중요하지가 않습니다. 이러한 상황에서 가장 중요한 문제가 바로 최적화입니다. 사실 최적화는 머신러닝 부분에서만 등장하지 않습니다. 대표적으로 linear regression이나 log-likelihood solution의 closed form이 존재하지 않을 때에도 결국 모수를 찾아내기 위해서는 수렴하는 값을 찾을 때까지 반복학습을 할 수 밖에 없기 때문입니다. 이 경우에도, 어떻게하면 빠르고 정확하게 최적화를 해나갈 수 있는지가 매우 중요합니다.
상황이 무엇이든, 결국 우리는 목적함수를 세우고 이를 최적화하는 과정을 거칠 수 밖에 없습니다. 이 때 목적함수는 주로 에러/비용이거나 정확도/이윤입니다. 각각의 경우 이를 maximize 혹은 minimize해줌으로써 원하는 결과를 얻습니다. 물론 generative adversary network와 같이 최적화가 minimax로 들어가는 경우도 있습니다. 이는 GAN이 서로 다른 두 모델을 동시에 학습하기 때문인데, 지난 포스팅에서 사실 이 조차도 결국 Jensen-Shannon divergence를 최소화하는 문제로 치환해서 푼다는 것을 확인한 바있습니다. 결과적으로 대다수 최적화 문제는 최댓값을 찾거나 최솟값을 찾는 형태입니다. 그리고 두 문제가 사실 부호를 바꿔주기만 하면 완전히 같은 상황으로 볼 수 있습니다.
따라서 어떤 알고리즘이 minimize를 빨리 그리고 정확히 할 수 있는가를 이해하는 것은 매우 중요합니다. 오늘은 이러한 알고리즘들 중에서 몇 가지를 소개하려고 합니다.
basic setups
| 다변수 함수 | 함수값이 하나의 실수값으로 나오는 함수 |
| 다변수 벡터함수 | 함수값이 벡터형태로 나오는 함수 |
보통 최적화를 해야할 목적함수는 비용이나 에러와 같은 하나의 실수값으로 나옵니다. 따라서 대다수 최적화 문제는 다변수 함수와 관련되어 있고, 알고리즘도 마찬가지입니다. 그러나 함수식이 여러개인 다변수 벡터함수도 중요합니다. 이는 regression과 관련이 깊습니다.
회귀란, 주어진 데이터들을 자신이 설정한 모델에 최대한 잘 피팅하는 일입니다. 이 때 기준이 되는 목적함수는 잔차라고 할 수 있으며, 데이터의 갯수만큼 함수식이 등장하게 됩니다. 따라서 이러한 경우에는 다변수 벡터함수의 최적화가 필요합니다.
 |
|---|
| 위의 문제는 7개의 함수식을 푸는 문제와 동일합니다. |
| Gradient | 다변수 함수에 대한 일차 미분 |
| Hessian | 다변수 함수에 대한 이차 미분 |
| Jacobian | 다변수 벡터 함수에 대한 일차 미분 |
 |
|---|
| 왼쪽: gradient. 오른쪽: Hessian |
 |
|---|
| Jacobian |
마찬가지의 이유로 Gradient와 Hessian은 비용이나 에러와 같이 하나의 값으로 값이 나오는 목적함수를 최적화할 때 등장합니다. 반면에 Jacobian은 종속변수와 설명변수 간의 관계식을 설정하는 회귀에서 주로 등장하게 됩니다. Jacobian과 Hessian은 모두 메트릭스 형태입니다. 차이점은 전자가 여러 함수들을 각각의 변수들로 한 번 편미분했다라고 하면, 후자는 하나의 함수를 각각의 변수들로 두 번씩 편미분했다는 차이가 있습니다. 전자는 일반적으로 non-symmetric하지만, 후자는 이차미분이 가능하다는 연속성이 미분 순서와 무관하다는 Schwarz’s theorem1으로인해 대칭행렬입니다.
Gradient Descent
가장 유명한 최적화 알고리즘입니다. 좋은 설명을 여러 곳에서 쉽게 접할 수 있으므로 핵심만 언급하고 넘어가도록 하겠습니다.

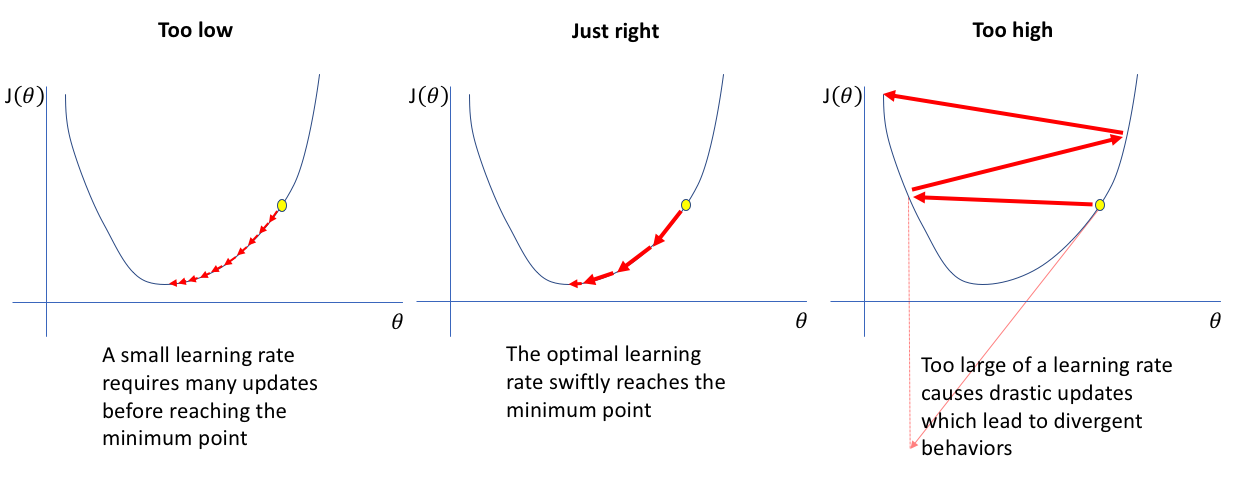
- 하이퍼파라미터()를 지정해주어야합니다.
- minimum 값에서 급격히 무뎌집니다.
1번, 는 한번에 얼만큼 내려올 것인가를 정하는 step size로 생각할 수 있습니다. 만약에 임의의 점에서 기울기가 어느 방향이든지간에 가파른 상태라면, 아무리 반복을 해도 수렴하지 못하게 됩니다. 오히려 반복을 할수록 실제 local minimum에서 멀어지는 일까지 발생할 수 있습니다. (통계학적으로 말한다면, 피셔정보량이 크기 때문에 계산하기 좋은 비용함수 - optimum에서 곡률이 작은 함수 - 임에도 불구하고 오히려 값을 못 찾는 경우라고 할 수 있겠네요.)
 |
|---|
| curvature, 곡률, 피셔 정보량 |
2번은 꽤나 중요한 문제입니다. gradient descent는 1차 미분을 활용하기 때문에 local minimum 근처에서 미분값이 0에 가까워집니다. 따라서 그 전까지 잘 내려오다가 정작 minimum 근처에서는 매우 조심스럽게 내려오는 태도를 보인다고 할 수 있습니다. 만약 곡률이 큰 함수라면, 답을 찾아내기 위해서 많은 반복시행을 요구하게 됩니다.
두 문제 모두, 비용함수의 곡률과 관련이 되있습니다. 곡률이 큰 함수라면, minimum 근처에서 수렴하기 어렵기 때문에 step-size가 커져야할 것입니다. 반대로 작은 함수라면 큰 step-size가 발산을 일으킬 수도 있기 때문에 조심해야합니다. 물론 이러한 논의는 가능한 모든 범위 안에서의 목적함수 모양을 모두 알고 있다는 가정 하에서 적절한 step-size를 추정하는 일이 될 것입니다. 결국 하이퍼파라미터를 사용자가 정해야한다는 점에는 여전히 큰 단점을 가지고 있는 것은 분명합니다.
물론 이를 위한 해결방법이 많이 연구되었습니다. 대표적으로 line search 방법을 활용한, backtracking line search나 golden section search 방법 등이 있습니다. 이와 관련해서는 아래 2을 확인하시면 됩니다.
algorithm for the numerical solution
gradient descent 방법이 neural network 덕분에 최솟값을 찾아내는 알고리즘으로 유명하지만, 사실 이 역시 어떤 선형방정식(linear system)의 근을 푸는 방법으로 활용될 수 있습니다. 방법은 아래처럼 linear least squares를 사용하는 것입니다. 물론 이 때에는 다변수 함수를 포함한, 다변수 벡터함수에 대한 이야기가 됩니다.

gradient descent가 quadratic 형태의 문제를 최소화하는데에 특화되어있다는 점을 활용했다고 생각하면 됩니다. 선형대수의 미분을 통해서 아래와 같이 변화량을 계산할 수가 있고 이를 통해서 방정식의 근을 반복적으로 찾아가게 됩니다.

하지만 실질적으로 어떤 방정식의 근을 찾기 위한 알고리즘으로는 conjugate gradient method를 많이 사용합니다. 위의 식에서 가 positive-definite하고 symmetric을 만족할 때, 미분을 하지 않고 반복시행으로 해를 구하는 방식입니다.
역행렬을 구하는 직접적인 계산이 어렵거나, 이를 위한 여러 분해법들을 적용하기에 가지고 있는 가 너무 sparse한 경우에 주로 활용됩니다. 자세한 예시는 위키피디아의 예시로 대체하는게 제일 좋을 것 같습니다.
Newton’s method
Newton’s method in calculus
미적분학에서 뉴턴법과 최적화이론에서 뉴턴법은 조금은 다른 의미를 가집니다. 먼저 일반적인 뉴턴법은 테일러 급수를 활용해서 함수의 근(root)을 찾을 때 사용하는 최적화 방식입니다. 다시 말해, 미분가능한 연속함수가 x축과 만나는 지점을 찾는 과정이라고 말할 수 있습니다. 일반적으로는 Newton-Raphson method3로 구분하여 수치해석분야에서 칭하는 것으로 알고 있습니다. 이 경우 Grandient descent와 동일하게 일계도함수까지만 활용합니다.


Newton’s method in optimization
함수의 최솟값을 찾아야하는 최적화 이론에서는 살짝 다르게 적용합니다. 원함수를 0으로 만드는 값을 찾는 것이 아니라, 기울기를 0으로 만드는 값을 찾는 것으로 바꿔주면 됩니다. 어떠한 minimum 값이든 반드시 기울기가 0이라는 점을 이용한 것에 불과합니다. 다시 말해, 미적분학의 뉴턴법을 한번씩 더 미분해줌으로써 간단히 해결해줍니다.

 |
|---|
| 임의의 점에서 같은 기울기를 가지는 이차함수로 원함수를 근사시키는 것과 동일합니다. |
위키피디아에서 핵심적인 내용만 간추려보면 아래와 같습니다.
- 이계도함수를 활용한다.
- 하이퍼 파라미터가 없다.
- minimum 근처에서도 빠르게 수렴한다.
앞선 gradient descent 방법을 모두 해결한 것처럼 보이지만, 사실 이 또한 불완전한 알고리즘입니다. 여라가지 단점이 있습니다.
- 두 번 미분가능해야한다.
- 변곡점 또는 이와 유사한 값이 존재해서는 안된다.
- 극대와 극소의 구분이 어렵다.
1번은 연산문제와 관련이 되어있습니다. 계산이 까다로운 경우에는 적용하기 어렵습니다. 그러나 다행히 neural network처럼 선형결합을 여러번 반복하는 모델들은 거의 대다수 두 번까지 미분이 가능합니다. 중요한 점은 변곡점이나 이와 유사한 값이 존재할 때에는 분모에 들어가는 값이 0 혹은 0에 가까운 값이 되면서, 정의되지 않거나 발산하는 문제가 발생한다는 점입니다.
3번 문제도 꽤 중요합니다. 고등학교 때 삼차함수를 미분해보면 알 수 있듯이 일계도함수의 근은 극대와 극소 모두에서 존재합니다. 이는 다시 말해, 내가 찾은 값이 엉뚱하게 local maximum이 될 수도 있다는 이야기입니다. 따라서 초기값을 여러군데 사용하거나 목적함수가 strongly convex function임을 밝히고 사용하는 경우들을 논문에서 종종 찾아볼 수 있습니다. 물론 gradient descent 방법은 분모 형태가 없기 때문에 이러한 문제에서 자유롭습니다. 그렇기 때문에 쉬운 예제들에서는 gradient descent 방법을 많이 사용합니다. 그러나 이를 보완한 훌륭한 방법들도 많이 존재합니다.
Multivariate Newton’s Method
다변수인 경우로 확장해도 newton’s method가 가지고 있는 단점과 장점은 그대로 유지됩니다. 앞에서는 변곡점이라고 했지만, 이제부터는 saddle point(안장점)가 존재할 때 수렴하지 않을 수 있습니다.

마찬가지로 이 때에도 이차미분을 실행하며, 변수가 여러 개이기 때문에 편미분을 해줍니다. 이때 다변수 함수의 이차미분 결과를 가리켜서 Hessian matrix라고 부릅니다.

Quasi-Newton method
다변수가 되면서 한가지 문제점이 발생합니다. 안 그래도 이계도함수를 구하는 과정이 연산량을 꽤나 필요로 하는데, 변수가 많아져서 행렬계산까지 해야하는 상황이 된 것입니다. 만약에 목적함수가 복잡하다면 사실 이계도함수를 구하는 것 자체가 불가능한 경우도 많습니다. 실제로 full Hessian matrix를 구하고 저장하는데 공간복잡도(메모리)는 가 필요합니다. 이렇게 되면, 변수가 많은 뉴럴네트워크 등에서는 사용하기가 힘들어집니다.
이런 경우를 해결하기 위해서 이계도함수를 근사적으로 구하는데, 이를 가리켜서 Quasi-Newton method(행렬을 근사적(Quasi)으로 구한다는 의미에서 기존의 Newton methods를 “full” Newton’s method라고 부릅니다.)라고 합니다. 물론 앞에서 다변수 벡터함수의 해를 구할 때, 등장하는 jacobian도 쉽게 구할 수 있습니다. 즉, Quasi-Newton method는 함수의 근을 찾거나 극점을 찾을 때 모두 사용할 수 있습니다. 다만 주로 근을 찾을 때에는 앞서 소개한 conjugate gradient method를 사용하고, 극값을 찾을 때에 Quasi-Newton method를 자주 사용합니다.
Quasi-Newton gradient에서 필요한 Hessian은 연속적인 gradient 벡터들을 통해서 업데이트됩니다. 즉 원래대로라면 2차 미분까지 해야하지만 1차 미분만을 합니다. 어떻게 근사하냐에 따라서 여러가지 방법들이 존재하는데 대표적으로 BFGS(Broyden–Fletcher–Goldfarb–Shanno algorithm) 등이 존재합니다. 이 분야도 내용이 쉽게 읽을 수 있는 부분은 아닌 것 같습니다. 다음번에 포스팅을 통해서 찬찬히 다뤄보도록 하겠습니다.
Gauss-Newton method
Gauss-Newton method는 최적화를 위한 뉴턴법 중에서도 다변수 벡터함수에 적합한 방식입니다. 다시 말해, non-linear least square 형태의 목적함수에 최적화되어있다고 볼 수 있습니다. 일반적인 least square를 사용하는 linear regression과 비교하며 설명하겠습니다.
non-linear least square와 동일하게 일반적인 선형회귀에서도 다음의 잔차 제곱의 합을 최소로 하는 모수를 구하고자합니다.


이를 구하기 위해서는 다음과 같은연립방정식을 풀어야합니다.

연립방정식인 이유는 위의 식이 모수의 갯수만큼 존재하기 때문입니다. 자연스럽게 다변수 벡터 함수식이 나오게 된 것이죠.
중요한 것은 잔차를 모수로 나눈 값을 구할 수 있느냐의 문제입니다. 일반적인 선형회귀식에서는 미분을 하고나면, p개의 모수 갯수만큼 p개의 연립방정식이 만들어집니다. 따라서 closed form이 존재하여 답을 구할 수가 있습니다. 하지만 미분을 하고나서도 변수의 갯수가 함수식보다 많거나 기타 등등의 이유로 해결이 되지 않는 경우가 많습니다. 이럴 때에 Gauss-Newton method를 활용해서 근사적으로 값들을 찾아나가게 됩니다.
조금더 구체적으로 찾아가는 과정은 밑에서 LMA 이야기를 하면서 진행하겠습니다.
Non-linear regression
하지만 만약 내가 피팅하려고 하는 모델이 선형식이 아니라면 이를 구할 수 있는 방법이 묘연합니다. 이 경우에는 아까 사용했던 netwon method in calculus를 활용합니다.

물론 자코비안 행렬로 바로 나눌 수가 없기 때문에 아래와 같이 행렬 P를 대신 구해서 구하도록합니다.

이 경우 행렬 P는 간단한 연산을 통해서 다음과 같음을 보일 수 있습니다. 자세한 과정은 위키피디아에 나와있습니다.


대표적으로 내가 가지고 있는 데이터가 원모양을 띄고 있다고 가정하고, 이 주어진 데이터를 바탕으로 원의 중심을 찾는 과정을 생각해보겠습니다. 원에 식을 세울 수 있지만 이는 알다시피 루트안에 제곱꼴로 들어간 수식이기 때문에 위에서처럼 closed form으로 답이 존재하지 않습니다. 따라서 이 대신에, gauss-newton method를 활용해서 잔차의 제곱을 줄여나갈 수 있습니다. 이 때에 내가 해줘야할 일은, 원의 중심점 (a, b)와 원의 반지름, r을 적당히 잡아주는 일만 하면 됩니다. 자세한 내용은 아래 추천자료 1번에 첨부하였습니다.
앞에서 gauss-newton method가 일종의 non-linear한 폼이나 closed form으로 해가 존재하지 않는 경우에만 쓴다고 이야기한게 아닌가 모르겠습니다. 이 방법은 당연히 linear한 경우에도 활용할 수 있습니다. 굳이 근사를 하는 이유는 우리가 가지고 있는 행렬 A가 너무 크거나, sparse해서 분해하기 쉽지 않을 때가 있을 것입니다. 이럴 때에도 근사를 위한 좋은 알고리즘으로 작동할 수 있습니다.
Levenberg-Marquardt
앞서서 Gradient descent는 항상 올바른 방향으로 내려가더라도 수렴값 근처에서는 굉장히 늦어진다고 했습니다. 반면에 Newton’s method는 수렴값 근처에서는 빠르게 움직이지만, 초기값을 잘못 잡으면 오히려 local maximum 값으로 이동할 가능성이 존재했습니다.
Levenberg-Marquardt 알고리즘(LMA, damped least-squares)은 gradient method 방법과 (gauss) newton’s method 방법을 적절하게 섞음으로써 두 알고리즘의 장점을 합친 것으로 이해할 수 있습니다. 수렴값과 현재 위치가 멀때는 gradient descent 방법을 사용하지만, 수렴값 근처에서는 newton’s method를 사용합니다. 두 알고리즘의 장점을 골라서 가지고 있는 탓에 실질적으로 가장 많이 쓰이는 알고리즘입니다. 물론, 가우스 뉴턴 방법과 동일하게 non-linear least squares 문제에서만 사용할 수 있습니다. 구체적인 수식은 다음과 같습니다.

여기에서 를 일컬어, damping parameter라고도 부릅니다. 만약 이 값이 커지면, gradient descent 방법에 가깝고, 작으면 Gauss-newton 방법에 가까워진다고 할 수 있습니다. 즉 이 damping 변수가 처음에는 컸다가 값이 개선됨에 따라 점차 작아짐으로써 두 모델의 장점을 취하는 형태입니다. 물론 처음보다 값이 개선되지 않으면 오히려 변수값이 커지기도 합니다.
조금 더 자세히 살펴보면 다음과 같습니다. 먼저 반복을 취할 때마다, 모수 는 새로운 추정치, 로 이동할 것입니다. 이 때 변화량은 linearization(gradient descent)으로 추정합니다.

즉, 이 때 위의 식에서 는 기존의 와 에 관한 식을 로 편미분한 자코비안으로 이해하면 됩니다. 이러한 1회 반복을 n차례 반복하되, 가지고 있는 데이터의 갯수가 m개 이므로 아래의 수식을 최소화하는 값을 찾는 것이 목표가 됩니다.

수식을 벡터 노테이션으로 바꾼 다음에 자코비안으로 미분을 해주면 아래와 같습니다.


사실 여기까지는 앞서 보았던 Gauss newton method와 동일합니다. 여기에서 LMA가 추가하는 것은 “damped” 변수를 추가하는 것입니다.

앞서서, 값이 작으면 GN 방법에 가깝다고 한 것을 확인할 수 있습니다. GN과 GD 방법들이 수렴값 근처에서 어떻게 속도차이가 나는가를 다시 생각해본다면, 이제 가 어떻게 변화하는 변수인지 이해할 수 있습니다. 만약 기준이 되는 잔차합, S 값이 개선이 되고 있다면, 큰 값을 유지합니다. 그러다가 개선폭 정도가 완화되면 작은 값으로 바꿔서 GN 방식으로 접근한다고 해석할 수 있겠습니다.
advantages
각주 및 추천자료
추천자료 / 참고자료
이 경우 함수의 근을 구하는데 필요한 계산의 시간복잡도는
 라고 합니다. ↩
라고 합니다. ↩

 라고 합니다.
라고 합니다.