NIPS(Neural Information Processing Systems)는 AI 연구자들에게 가장 각광받는 행사로, 그 해의 의미가 큰 논문을 발표하고 의견을 나누는 행사입니다. 2016년에는 이안 굿펠로우가 자신이 2014년에 소개한 GAN에 관하여 발표를 진행했었습니다. 이 글에서는 arXiv에 제출된 NIPS 2016 Tutorial:Generative Adversarial Networks 글을 리뷰합니다. 특히 그 중에서도 generative model에 관해서 중점적으로 다뤄보고자 합니다.

Generative models

generative model이란, 입력받은 데이터와 유사한 새로운 데이터 샘플들을 생성(generate)해내는 모델입니다. 아래와 같이, 이미지 데이터를 입력받으면 이와 유사한 이미지들을 추출해내는 것이 가장 대표적인 예시입니다.

generative model 예시1

이안 굿펠로우는 NIPS 2016 Tutorial:Generative Adversarial Networks에서 generative model을 아래와 같이 설명했습니다.

• any model that takes a training set, consisting of samples drawn from a distribution $p_{data}$, and learns to represent an estimate of that distribution somehow.

즉, generative model의 핵심은 data generating process를 찾는 것으로 이해할 수 있습니다. data generating process란, 가지고 있는 데이터를 더 이상 주어진(given) 것이 아니라, 특정한 분포를 따르는 확률변수로 바라보는 관점입니다. 이 때 data가 따르는 분포를 가리켜서 $P_{data}$라고 합니다. $P_{data}$는 실제로 알 수가 없기 때문에 모델들은 이를 추정해냅니다. 이 때 모델이 추정해낸 분포를 가리켜서 $P_{model}$이라고 부릅니다. 따라서 좋은 generative model은 학습한 분포, $P_{model}$이 $P_{data}$를 잘 추정해내어서, 이로부터 generate하는 샘플들이 실제 data와 유사한 경우를 뜻합니다.

Taxonomy of deep generative models

자연스럽게 우리는 어떻게 $P_{model}$를 정의함으로써 $P_{data}$를 잘 추정해낼 수 있는가의 문제로 들어서게 됩니다. 이를 위해 다양한 방법들이 연구되어왔지만, 일반적으로 아래와 같은 분류그림을 통해 이들을 설명합니다.

Taxonomy of deep generative models

Explicit & Tractable density

첫 번째 방법은 직접적으로(explicitly) $P_{model}$을 표현하는 방법입니다. 보다 정확히 말하면, density를 수식으로 ‘정의할 수 있는’ 모델들을 뜻합니다. 아주 쉬운 예시로 대한민국 성인남성 키에 대한 일부자료를 가지고 있다고 생각해보겠습니다. 이 데이터가 정규분포($P(x; \theta)$)를 따를 것이라고 가정하고 모수($\theta$)를 추정했다면, 이를 가리켜서 explicit하게 분포를 표현했다고 이야기합니다. 이 때 $P_{model}$은 키에 대한 분포로 추정해낸 정규분포가 됩니다. 이처럼 density를 학습할 때 수식으로 ‘정의’할 수 있을 뿐 아니라, 수학적으로도 미분, 적분 등이 가능한 분포를 tractable density라고 이야기합니다.

따라서 tractable density는 maximize likelihood 방법을 이용해서도 충분히 $P_{model}(x; \theta)$의 모수를 추정할 수 있습니다. 위의 예시에서처럼 정규분포로 모델을 정의했다면 이는 log-likelihood가 미분가능하고, mle 추정량으로 sample mean과 sample variance로 나온다는 것을 쉽게 도출할 수 있습니다. 이처럼 tractable density는 모델이 직접 계산 가능하기 때문에 모든 변수에 대한 세밀한 조정이 가능하다는 장점이 있습니다.

그러나 수학적으로 계산이 쉽다고 해서 반드시 ‘키’와 같은 1차원 데이터만 학습할 수 있는 것은 아닙니다. 한 때, generative model에서 가장 중요한 위치를 차지하기도 했던 PixelCNN은 이미지에 대한 분포로 tractable한 분포를 정의함으로써 이미지 데이터를 생성해냈습니다.

pixelCNN2

PixelCNN은 mle를 계산할 수 있기 위해서, 몇 가지 가정을 합니다. 예를 들어, 이미지에는 픽셀 값들 사이에 일정한 순서가 존재하고 이를 바탕으로 mle를 이전 픽셀 값들을 조건으로 하는 i번째 조건부 확률의 곱으로 표현가능하다고 생각합니다. 그리고 이를 위해서 masked convolutional layers 등을 사용합니다. 자세한 내용은 [이곳] (https://towardsdatascience.com/autoregressive-models-pixelcnn-e30734ede0c1)에서 확인할 수 있습니다.

이처럼 tractable한 분포를 사용하기 위해서는 모델에 강력한 제약을 걸어줄 수 밖에 없습니다. 결국 데이터가 복잡해질수록, 이러한 조건들이 성능을 떨어뜨리게 만듭니다. PixelCNN이 새롭게 출현한 VAE와 GAN 등에 밀려서 점차 사라져가는 이유가 바로 이 때문입니다.

Explicit & Approximate density

이러한 단점을 보완하고자 제약을 없애고 더 복잡한 모델을 사용하는 것이 intractable한 density로 $P_{model}$을 표현하는 방법입니다. 여전히 수식으로 정의내릴 수는 있다고 하더라도, 더 이상 계산이 불가능하기 때문에 density를 근사해서 쓸 수 밖에 없습니다. 이 때문에 이러한 종류의 generative model을 approximate density라고 부릅니다. 그러나 결국에는 근사한 density를 최적화하는 일이 likelihood를 최대화하는 것과 동일하다는 점을 확인할 수 있습니다.

이 방법을 사용하여 이미지 데이터를 생성하는 것이 그 유명한 VAE(Variational Autoencoder)입니다. VAE를 완벽히 이해하기 위해서는 필요한 기본 지식들이 많이 있기 때문에 다른 포스팅에서 더 자세히 다루겠습니다. 간단히 내용을 요약하면 다음과 같습니다.

Variational Autoencoder3

먼저, VAE에서 중요한 개념은 Autoencoder입니다. Autoencoder란, 입력받은 데이터를 z라는 코드로 압축하되, 그 z가 x를 그대로 복원할 수 있는 neural network를 의미합니다. 여기서 z는 단순히 입력값보다 차원이 낮은 deterministic한 data(상수 벡터)에 해당됩니다.

autoencoder4

VAE는 이러한 autoencoder에서 code “z”의 분포를 구하는 과정으로 이해할 수 있습니다. 이렇게되면 관심을 가지게 되는 모수는 더 이상 $\theta$가 아니라 새로운 변수(latent variable, z)가 됩니다.⁵ 구체적으로, encoding model에서는 $P_{\theta}(z\mid x)$를, decoding model에서는 $P_{\theta}(x\mid z)$를 구성하게 됩니다.

베이즈 관점에서 $P_{\theta}(z\mid x)$는 posterior 분포라고 부릅니다. 문제는 이를 구하는 것이 매우 어렵다는 점입니다. 베이즈 정리에 따르면, $P_{\theta}(z\mid x) = P_{\theta}(x\mid z)P_{\theta}(z)/P_{\theta}(x)$입니다. 하지만 분모의 $P_{\theta}(x)$를 계산하기가 불가능할 뿐만 아니라 애당초 latent distribution, $P(z)$를 알지 못하는 상황이기 때문에 z에 대해 적분을 할 수가 없는 상황입니다. 이러한 문제를 해결하기 위해서, variational inference(VI)를 사용합니다.

VI란, 이상적인 확률분포를 모르기 때문에 이를 추정하기 위해서 다루기 쉬운 분포($q_{\Phi}(z\mid x)$)를 근사하여 대신 사용하는 방법론입니다. VI를 사용하면 큰 장점이 있는데, 결국 likelihood를 최대화하는 문제가 closed form으로 구해지는 함수식을 최소화하는 최적화 문제와 같아진다는 점입니다. 이렇게 되면, 함수식이 아무리 복잡할지라도, neural network를 통해서 수렴해갈 수 있기 때문에 문제가 해결이 되는 것입니다.⁶ 이번 글에서는 언급하지 않았지만, nn을 사용하기 위해서 reparameterization trick을 활용한다는 점도 중요한 특징 중 하나입니다.

정리하면, VAE는 복잡한 모델을 아래와 같은 몇 가지 가정을 바탕으로 근사적으로 구해냄으로써 최대한 $P_{model}$이 $P_{data}$와 유사하도록 만들어줍니다. 이번 글에서는 언급하지 않았지만,

VAE : Model Specification7

Implicit density

이제 돌아와서 Implicit density에 대해서 간단히 설명하고자 합니다. 맨 앞에서 ‘키’를 예시로 들었던 적이 있습니다. 우리가 explict하고 tractable한 방법을 선택해서 ‘키’를 정규분포로 설명했다고 가정해보겠습니다. 이 경우, 어느 누군가 “키”에 대해서 묻는다고 해도 우리는 평균과 표준편차라는 단 두 개의 숫자만을 가지고 데이터의 분포를 설명할 수 있습니다.

하지만 누군가 “키”에 대해서 물어본다면 평균과 표준편차를 알고 있어야만 대답할 수 있는 것은 아닙니다. ‘키’가 $P_{키}(x)$를 따른다고 하면, 이를 똑같이 따르는 다른 샘플들을 제시해주는 것도 답변이 될 수 있습니다. 이러한 방법을 가리켜서 “implict“하게 P_{data}를 표현했다고 말합니다. 다시 말해서, $P_{data}$ 분포를 따르는 새로운 변수들을 계속해서 뽑아낼 수 있다면(generate), 이 역시도 분포를 표현하는 하나의 방법이 되는 것입니다.

물론 의미있는 설명이 되려면, 단 두 개의 숫자만 필요하던 앞의 예시와 달리, 훨씬 많은 샘플들이 필요하기 때문에 비효율적이라고 할 수 있습니다. 하지만 대부분 generative model은 1차원의 데이터가 아닌 3차원 이상의 데이터들을 많이 다룹니다. 이처럼 데이터가 복잡해질 수록, tractable한 분포를 계속 고집하는 것이 틀릴 수가 있습니다. 그렇기 때문에 계속해서 새로운 변수들을 뽑아낼 수 있는 분포, $P_{model}$을 가지고 있는 것이 때로는, $P_{model}$을 수식으로 정의내리거나 이를 계산할 수 있는가에 대한 여부를 따지는 것보다 더 중요할 수 있습니다.

가장 대표적인 Implicit density가 그 유명한 Generative Adversarial Networks(GAN)입니다. 이에 대한 내용은 아예 다른 포스트에서 자세히 다루도록 하겠습니다.

Generative Adversarial Networks로 생성해낸 인물 사진

결과적으로 generative model은 이안 굿펠로우의 말대로 어떻게든(somehow) $P_{model}$을 표현(represent)할 수 있도록 모델을 잘 학습시키는 것이 중요합니다.

Why generative modeling is worth studying.

다시 돌아와서, NIPS 2016 Tutorial:Generative Adversarial Networks의 이야기를 이어가려고 합니다. 이 곳에서는 특히 implicit density가 중요한 이유에 대해서 좋은 아이디어를 많이 언급하고 있습니다. 요약하면 데이터를 generate하는 것만 가능할지라도, 다음과 같은 이유로 매우 중요하다고 할 수 있습니다.

1. high-dimensional probability distribution

high-dimensional probability distribution은 많은 응용수학과 공학에서 매우 중요한 주제입니다. generative model을 학습시키고 샘플링하는 일이 이런 고차원 확률분포에 대한 검정을 해줄 수 있습니다.

1. reinforcement learining

generative model은 특히 모델 기반의 강화학습에 큰 도움을 줄 수 있습니다. 예를 들어, 시계열 데이터에 대한 generative model은 가능한 결과값들을 시뮬레이션함으로써 조건부 기대분포를 구하는데 활용될 수 있습니다.

1. semi-supervised learning

최근 딥러닝 알고리즘이 잘 작동하기 위해서는 기본적으로 라벨링이 되어 있는 트레이닝셋이 존재해야합니다. 이 때문에 실질적으로 적용가능한 경우는 많지 않을 수 있습니다. 하지만 generative model은 결측치가 있는 데이터로 학습이 가능하기 때문에, 만약 input 데이터가 결측치를 가지고 있더라도 예측을 해낼 수가 있습니다. 이 때문에 generative model을 잘 활용하면, semi-supervised learning이 가능해집니다.

1. multi-modal outputs

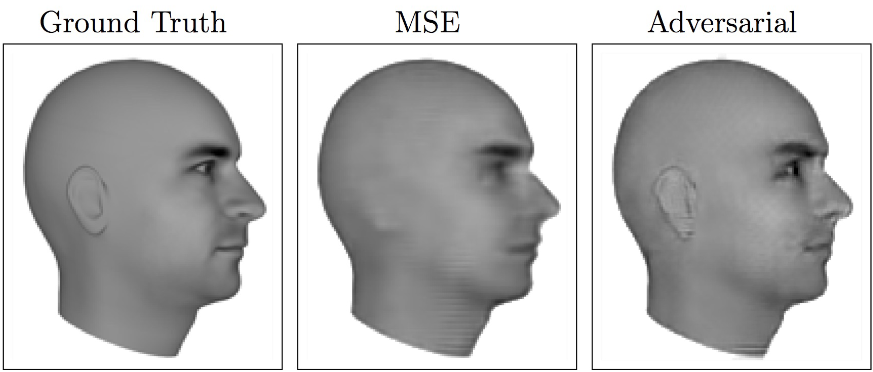
전통적인 머신러닝에서는 하나의 인풋에 대해서 하나의 결과값이 나오게끔 학습합니다. 하지만 하나의 인풋에 대한 정답이 반드시 하나만 존재하지 않는 경우도 많습니다. 대표적으로 동영상에서 다음 장면을 예측하는 일은 여러 개의 복수 정답이 존재하는 문제입니다. 이처럼 multi-modal한 결과값을 다루기에 generative model, 특히 GAN이 잘 작동합니다.

1. realitic generation of samples

마지막으로 실제로 어떤 분포로부터 샘플을 만들어내는 일이 필요한 경우가 굉장히 많습니다. 대표적으로 single image super-resolution이 있습니다.

각주 및 추천자료

추천자료

1. VAE 수식 증명

2. 데이터사이언스랩 심화스터디 - 손진원

3. generative model 한글 자료

각주