지난 포스팅에서는 알고리즘 분석에 필요한 개념들을 설명했습니다. 사실 이를 통해 배우고 싶었던 것은 오늘 다룰 P, NP 등의 개념들입니다. 이번 글은 지난 포스팅의 내용을 모두 숙지했다는 상태로 진행하겠습니다.

머신러닝 논문을 읽다보면 모르던 용어들을 마주칠 때가 있습니다. 알고리즘이나 자료구조와 같은 과목을 수강해본 적이 없는 저로써는 그럴 때마다 당황스러울 때가 많습니다. 오늘은 그 중에서 NP-hard problem과 이를 이해하기 위해 필요한 개념들에 대해 간단하게 적어보고자 합니다.¹

NP-hard problem in Data Science

Pattern Recognition 학술지에 기재된 Data clustering: 50 years beyond K-means 글을 읽다가 아래와 같은 문구를 발견했습니다.

1

Minimizing this objective function is known to be an NP-hard problem(even for K = 2).

NP-hard 문제가 무엇인지는 모르지만, 대충 k-means 클러스터링의 local optima에 관한 내용이겠거니 추측은 할 수 있습니다. 그렇지만 어물쩍 넘어가기에는 찝찝할 수밖에 없습니다. NP-hard problem은 컴퓨터 공학에서 큰 비중을 차지할 뿐만 아니라, 그 근간은 알고리즘에 대한 이해에 있기 때문입니다. 따라서 비단 논문이나 학술지를 읽을 때만을 위해서가 아니라, Machine Learning을 제대로 이해하기 위해서는 P, NP 등의 개념을 배워보는 것이 꽤나 중요한 일이라고 생각합니다.

오늘은 이를 이해하기 위한 개념들을 차근차근 살펴보면서 감을 잡아보려합니다.

Class P/ NP

먼저 P, NP가 무엇인지부터 확인해보겠습니다.² 아래의 정의에 포함된 polynomial time이 궁금하신 분은 지난 포스팅을 참고해주시기 바랍니다. 추가적으로 decision problem이란, 어떤 문제에 대한 대답이 yes와 no로 구분되는 문제를 의미합니다. 예를 들어서 “두 숫자 x와 y가 있을 때 y는 x로 나누어떨어지는가?” 라는 문제는 예와 아니오로 답이 존재하는 전형적인 결정문제에 해당합니다.

The general class of questions for which some algorithm can provide an answer in polynomial time is called “P”

NP is the set of decision problems for which the problem instances, where the answer is “yes”, have proofs verifiable in polynomial time by a deterministic Turing machine.

보다 쉽게 설명드리면, 어떤 문제에 대해서 polynomial time algorithm이 존재하면 해당 문제를 P집합의 원소로 받아들이는 것입니다. 오해하기 쉬운 부분은 알고리즘이 아니라, 해당 “문제”가 P에 속한다는 것입니다. 예를 들어서 sorting하는 문제를 생각해보겠습니다. 지난 포스팅에서도 봤지만 버블 sorting은 $n^2$이라는 다항식으로 표현되는 시간복잡도를 가지고 있습니다. 따라서 sorting하는 문제는 polynomial time 알고리즘을 제시할 수 있으므로 P 문제에 속하게 됩니다. 추가적으로 정확한 명칭은 “deterministic” polynomial time입니다. 즉 동일한 input에 대해서 다항시간 이내에 같은 결과로 풀리는 것이 “증명”된 혹은 확실히 말할 수 있는 문제들을 의미합니다.

반대로 NP란, “non”deterministic polynomial time 알고리즘을 가지는 문제들을 의미합니다. 알고리즘이 nondeterministic하다는 것은 동일한 input에 대해서 다른 결과값이 나온다는 것을 의미하는데 사실 이를 직관적으로 이해하기란 쉽지 않습니다. 간단한 예시로는 두 지점 a와 b 사이의 이동경로를 결정하는 알고리즘을 생각해볼 수 있습니다. 보통 최단거리를 구하는 문제는 정답에 해당하는 경로를 특정할 수 있기 때문에 결정적 알고리즘에 해당합니다. 그러나 최장거리에 대해서는 정확한 값(과정)을 정의할 수가 없게 됩니다. 즉, 똑같은 a와 b의 input을 주어도 그 결과값이 매번 같지 않을 수 있는 것입니다. 그럼에도 불구하고 “알고리즘”이라고 부를 수 있는 이유는 그 과정을 모르더라도 결과적으로는 목적지에 도착할 수 있다는 사실은 알고 있기 때문입니다. 따라서 어떤 문제가 “non”deterministic polynomial time 알고리즘이 존재한다는 것은, 그 정확한 값이 다항시간 안에 풀릴 수도 있고 때로는 안 풀릴 수도 있지만 그 결과를 계산할 수는 있는 알고리즘이 존재한다고 이해할 수 있습니다.

다행히도 복잡한 위의 정의 대신, NP는 또 다른 정의를 가지고 있습니다. 두 정의는 표면상 달라보이지만 사실 둘은 같은 의미를 가집니다. 이에 대한 설명은 계산 복잡도 이론에 대한 공부가 더 필요한 것으로 보여집니다. 이번 글에서는 두 정의가 동일함을 받아들이고 글을 이어나가겠습니다. 그리고 사실 이번 글을 자주 읽다보면, 두 정의가 결국 같은 말을 하고 있음을 이해할 수 있는 것 같습니다. 좀 더 쉬운 정의는 아래와 같습니다.

문제가 주어지고, 해당 문제에 대해 어떤 suggested solution이 주어졌을 때, 다항시간 안에 그 solution이 맞는지 아닌지 구분할 수 있는 문제.

NP에 대한 위의 정의를 예를 들어서 설명하도록 하겠습니다. 해당 예시는 이 곳의 블로그에서 사용한 예제입니다.

다리 건너에 보물이 가득한 섬이 있습니다. 보물들은 각각의 무게와 값어치가 표시되어 있으며, 여러분은 이를 가져올 수 있는 가방도 가지고 있습니다. 그런데 두 가지 제약 조건이 있습니다. 첫째 다리가 버틸 수 있는 무게가 100kg입니다. 둘째 가지고 와야할 보물의 값어치가 반드시 2억 이상이어야합니다. 만약 위의 조건을 모두 만족한 채 보물을 챙겨서 가지고 나올 수 있을까요?

이러한 문제는 역시 결과가 yes와 no로 나뉘기 때문에 결정문제에 속합니다. 만약 이를 풀 수 있는 유일한 알고리즘이 전체 N개의 보물을 조합해가면서 제약 조건을 만족하는 보물을 일일이 찾아내는 방법뿐이라고 가정을 해보도록 하겠습니다. 각각의 보물들을 가방에 넣었다가 뺐다를 반복하는 위의 알고리즘은 전체 가지수 N으로 인해 $2^N$의 조합 갯수를 가지게 되고, 따라서 $O(2^N)$의 시간복잡도를 갖습니다. 따라서 N이 조금이라도 커지게 되면 running time은 걷잡을 수 없이 오래 걸리는 알고리즘을 가지는 문제가 됩니다. 적어도 위의 문제는 현재 알고리즘으로는 P 집합에는 속하지 않음을 알 수 있습니다.

그렇지만 누군가 solution을 추천해준다면 이야기가 달라집니다. 예를 들어 누군가가 가방에 담을 보물이 적힌 종이(suggested solution)를 줬다고 생각해봅시다. 만약 그렇다면 우리가 할 일은 suggested solution대로 가방에 담은 뒤에 보물들의 값어치와 무게를 누적합하면 됩니다. 당연히 다항시간 안에 누적합을 할 수 있으며, 손쉽게 해당 조합이 문제의 정답이 되는지 아닌지를 구분할 수 있게 됩니다. 이러한 문제는 따라서 NP 집합으로 분류할 수 있게 됩니다.³

마지막으로 한가지 집고 넘어가야할 점은, 두 번째 정의를 이용한다면 P와 NP 집단의 포함관계를 쉽게 확인할 수 있습니다. P 집합 문제는 정확한 답을 이미 다항시간 안에 풀 수 있는 문제에 해당합니다. 따라서 누군가 솔루션을 추천해준다면 이를 통해서 결과를 확인하는 것도 당연히 다항시간 안에 이뤄지게 됩니다. 따라서 결론적으로 P는 NP의 부분집합이 되게 됩니다.

Reduction

다음으로 NP-Hard와 NP-Complete 문제를 이해하기 위해서는 문제들 간의 reduction 관계를 이해할 필요가 있습니다. 예를 들어 문제 X가 문제 Y로 reducible하다는 것은, Y문제를 풀어주는 알고리즘을 이용해서 X를 풀 수 있는 또 다른 알고리즘을 찾아낼 수 있음을 의미합니다. 따라서 X가 Y로 reduction이 된다는 것은, Y문제를 풀 수 있다면 우리는 X 문제들도 해결이 가능하다는 의미가 됩니다. 그렇기때문에 Y 문제가 보통 더 어려운 문제로 해석하게 됩니다. 물론 reduction의 관계가 반드시 일방향으로만 존재하는 것은 아닙니다. X가 Y로 reduce될 수도 있지만 반대로 Y도 X로 reduce될 수 있는 것입니다. 이 경우에 두 문제의 난도는 동일 수준으로 해석하게 됩니다.

NP-Hard, NP-Complete

NP-Hard 문제란, NP 클래스 안에 있는 모든 문제가 reducible할 수 있는 문제를 의미합니다. 즉 어떤 문제를 풀 수 있어서, 그 문제를 가지고 NP 집합 안의 모든 문제를 해결할 수 있다면 우리는 그 문제를 NP-hard라고 부르게 됩니다. 몇 가지 오해하기 쉬운 부분들을 짚고 넘어가겠습니다. 첫째, NP-Hard 문제는 여러개 존재할 수 있습니다. 예를 들어서 NP 클래스를 초등학교 수학 문제라고 가정해보겠습니다. 만약 중학교 수학문제를 풀 수 있다면, 초등학교 수학문제를 모두 풀 수 있을 것입니다. 그렇게 되면 중학교 수학문제도 NP-hard 문제가 됩니다. 당연히 고등학교, 대학교 수학문제들도 해당 집합에 포함이 될 수 있으며, 이렇듯 여러 원소를 가지는 집합으로 인식할 수 있습니다.

두번째로, NP-hard 문제 역시 NP 집합에 속할지 속하지 않을지는 알 수 없다는 사실입니다. 어떤 NP-hard 문제는 똑같이 NP 집합에 속할 수 있지만, 어떤 문제는 속하지 않을 수도 있습니다. 위에서 사용한 초등학교 예시를 이어서 설명해보겠습니다. 만약 초등학교 6학년 기말고사 수학문제를 풀 수 있으면, 초등과정의 모든 수학문제를 풀 수 있게 된다고 생각해보겠습니다. 이렇게 되면 해당 문제는 NP-hard 이면서 NP 집합에 속하게 됩니다. 반면에 중학교 이상의 문제들은 NP 집합에 속하지 않으면서 NP-hard 문제로 남게됩니다.

NP-Complete은 바로 전자에 해당하는 경우입니다. 즉, 모든 NP를 풀 수 있는 알고리즘을 가지고 있는 NP-hard 문제 역시도 NP 집합에 속하게 될 때를 가리켜서 NP-Complete 이라고 부릅니다. 위의 설명을 하나의 그림으로 표현하면 아래와 같습니다.

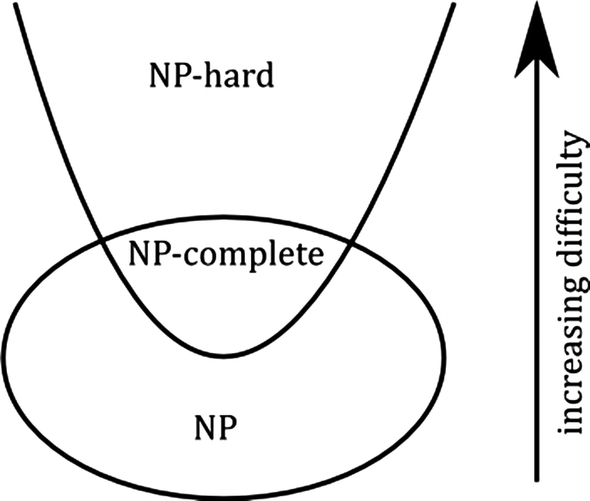
앞에서 NP 문제임을 보이는 것은 두번째 정의를 이용하면 매우 간단했습니다. 다항시간 안에 결과를 확인할 수 있는, 임의의 정답을 하나 찾아낼 수만 있으면 되기 때문입니다.⁴ 따라서 많은 NP-Hard 문제들 중에서 NP-complete임이 밝혀진 문제들이 존재합니다. 대표적으로 Travelling salesman problem 등이 있지만 이 곳에서 다른 많은 문제들도 확인할 수 있습니다.

P versus NP problem

이제 중요한 문제가 하나 남아있습니다. 앞에서 NP-Hard 그리고 그 속에 속하는 NP-Complete는 모든 NP 문제들이 reducible한 문제들임이라고 증명했습니다. 즉, 이 문제들을 다항시간 안에 풀 수 있게 되면 모든 NP 문제들도 다항시간 안에 풀 수 있는 알고리즘을 찾을 수 있게 되는 것입니다. 따라서 Traveling Salesman 문제와 같은 NP-Complete 문제들 중 어느 것 하나만이라도 다항시간 내에 풀 수 있음을 증명하게 된다면, 모든 NP 문제들이 P 문제가되게됩니다. 반대로 풀 수 없음을 증명하게 된다면 상황은 달라질 것입니다. 이를 간단하게 그림으로 나타내면 아래와 같습니다.

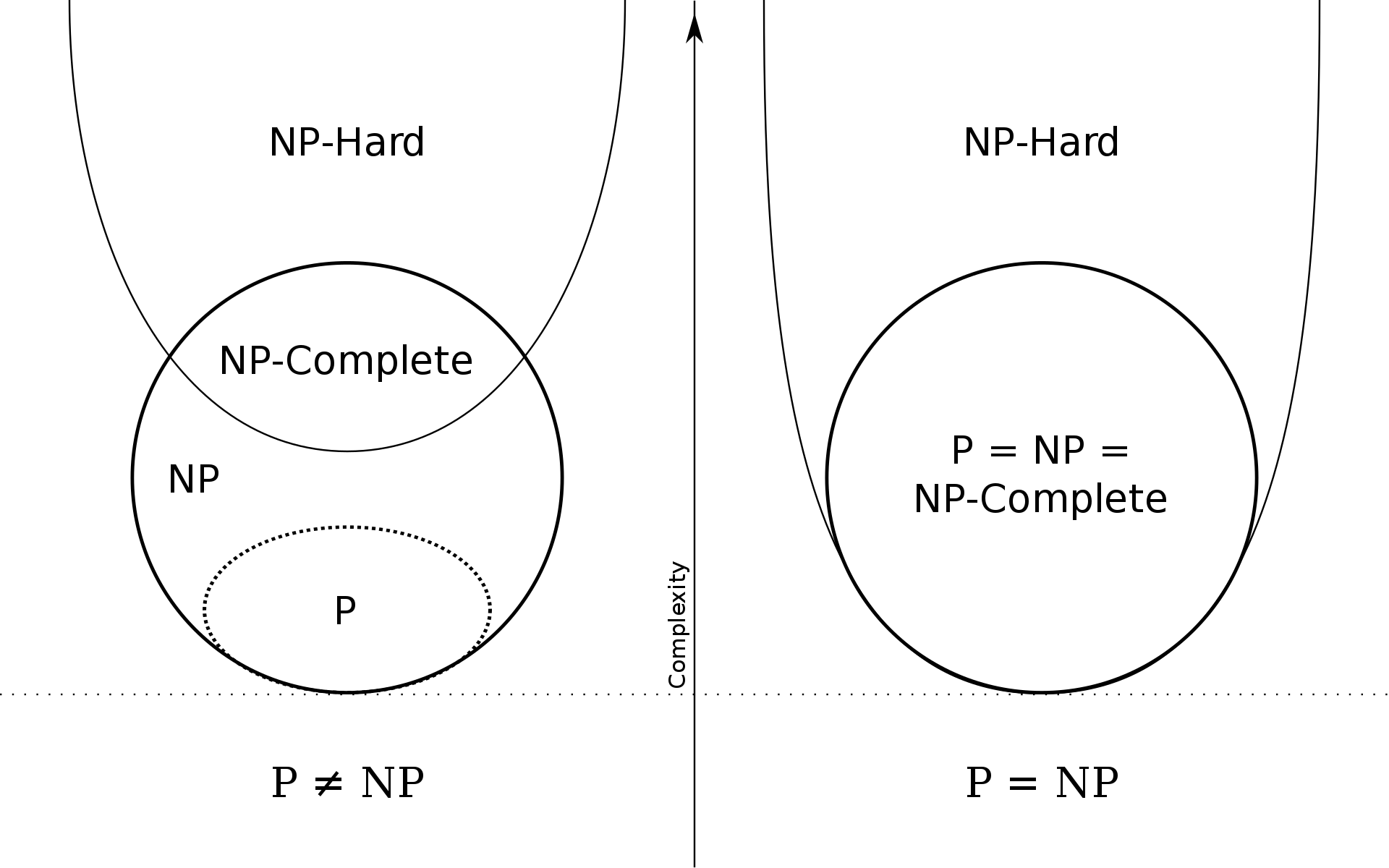
그리고 바로 이 문제가 그 유명한 P-NP 문제입니다. 21세기 수학계에 큰 발전을 가져올 수 있는 밀레니엄 문제 중에 첫 번째 미해결 문제입니다. 이는 비단 일반인들과 동떨어진 문제만은 아닙니다. 현재 대다수 보안 알고리즘은 NP-Complete에 기반으로 만들어졌다고 합니다. 만약 P=NP로 증명이 된다면 보안 회사의 암호화 문제들은 모두 다항시간 안에, 다시 말해 충분히 현실가능성 있는 시간 안에 풀어버릴 수 있는 문제가 되버립니다.

NP-hard problem in Data Science

다시 돌아와서 원래 제가 NP-Hard 문제를 접했던 문제를 다시 확인해보겠습니다.

Minimizing this objective function is known to be an NP-hard problem (even forK=2)(Drineas et al., 1999). Thus K-means, which is agreedy algorithm, can only converge to a local minimum, eventhough recent study has shown with a large probability K-meanscould converge to the global optimum when clusters are well sep-arated (Meila, 2006).

다시 살펴보면, k-means의 목적함수를 최소화하는 것에 대한 아래와 같은 해석이 가능합니다. 먼저 해당 문제는 다항시간 안에 풀리지 않는 어려운 문제입니다. 이를 해결하게 되면, 다른 모든 NP문제들도 다항시간 안에 해결할 수 있게 됩니다. 하지만 아직까지는 모든 데이터에 대해서 실제 최솟값을 확인하는 일이 다항시간 안에 이뤄지지 않다고 보는 편이 맞습니다. 따라서 뒷 문장에서 언급되어있듯이 local minimum을 찾는 것으로 대체하게 됩니다.

이처럼 Machine Learning 문제를 해결하다보면, 해당 문제가 NP complete problem인 경우가 많이 존재합니다.⁵ 따라서 많은 경우에 이를 대체하여 해결하기 위한 방법들을 연구하고 있습니다. local optimum으로 해결하거나 문제를 살짝 변형해서 polynomial time 안에 구하는 등으로 변경하는 것이 그 방법 중 하나입니다. Machine learning을 공부함에 있어서 algorithm에 대한 이해가 매우매우 필수적인 이유라고 생각이 드는 부분이기도 합니다.

각주 및 추천자료

추천자료

1. http://sanghyukchun.github.io/60/
2. https://zeddios.tistory.com/93?category=682196

각주