어떤 문제를 해결하기 위한 방법은 다양합니다. 예를 들어 Bubble sort, Quick sort, Merge sort와 같은 알고리즘들은 모두 임의의 숫자들을 크기 순서대로 재배열해줍니다. 그러나 알고리즘의 작동 방식이 모두 다르기 때문에, 문제해결에 필요한 시간과 메모리 양은 모두 다를 것입니다. 이러한 알고리즘 간의 차이를 이해하는 것은 프로그래밍에 매우 중요합니다. 똑같은 결과를 반환하더라도, 더 좋은 알고리즘을 찾아내고 이를 계속 발전시켜나감으로써 더욱 어려운 문제를 해결할 수 있게 되기 때문입니다.

Algorithm Analysis

좋은 알고리즘과 나쁜 알고리즘을 구분하는 기준은 효율성입니다. 효율적인 알고리즘이란 기본적으로 execution에 필요한 resources 양이 적은 프로그램을 뜻합니다. 과연 프로그램을 실행하는데 필요한 자원은 어떤 것이 있을까요? communication bandwidth 등도 필요하지만 다음의 두가지 자원이 가장 중요하게 다뤄집니다.

1. 메모리
2. running time

두 가지 자원은 각각 공간과 시간의 개념으로 알고리즘 분석에 해석이 됩니다. 더 적은 공간과 짧은 시간을 필요로 할수록 효율적인 알고리즘이라고 판단하는데, 이는 각각 메모리 사용량이 작고, 동작시간이 짧은 것을 의미하게 됩니다. 그러나 두 개념이 때로는 상충되는 상황이 발생할 수도 있습니다. 즉, 메모리가 조금 많이 필요로 하지만, 시간이 적게 걸리는 알고리즘이 있는 반면, 시간은 많이 걸려도 필요한 공간은 작은 경우가 있습니다. 이런 경우에 일반적으로 메모리보다 계산시간을 더 중요시여깁니다. 메모리나 bandwidth는 돈을 주고 살 수 있지만, 시간은 돈을 주고도 살 수 없기 때문일 것입니다. 그래서 대다수 알고리즘 분석은 running time을 추측(estimate)하는데 목적을 두고 있습니다. 우리는 이러한 분석을 통해서 좋은 알고리즘을 선별하고 계속해서 발전시켜 나가게 됩니다.

time complexity

앞서서 running time에 대한 분석을 가리켜 time complexity(시간복잡도)라고 부릅니다. 그런데 사실 계산시간을 비교하는 것은 실행환경에 크게 영향을 받습니다. 예를 들어, 컴퓨터 사양이 좋고, data set 크기가 작으면 아무리 나쁜 알고리즘이더라도 계산시간은 얼마 안 걸리기 때문입니다. 반대로 좋은 알고리즘이 사용하고 있는 프로그램 언어 때문에 계산시간이 커질 수도 있습니다. 따라서 running time을 estimate할 때에는 실행시간을 측정하는 대신, 연산에 필요한 실행 횟수를 계산합니다. python 언어를 바탕으로 한 간단한 예제들을 살펴보겠습니다.

1
2
3
4
5

def sum(a, b) :
    res = 0
    for i in range(a, b):
        res = res + i
    return res

위의 함수는 입력받은 두 수 사이에 있는 값들을 더해주는 알고리즘입니다. 찬찬히 살펴보면 위의 알고리즘은 res = 0과 res = res + i를 각각 한 번씩 실행해주고, for 구문 안의 2줄은 각각 N번씩 실행하도록 설계되어있습니다. 여기에서 N이란, 입력받은 두 수(a, b) 사이에 존재하는 상수 갯수를 의미합니다. 따라서 해당 연산에 필요한 전체 실행 횟수는 2N+2가 됩니다. 중요한 점은 2N+2라는 실행횟수가 언제나 동일하다는 점입니다. 그런데 아래와 같은 예제에서는 이처럼 간단하지 않습니다.

1
2
3
4
5
6

def bubble(lst) :
    for i1 in range(0, n) :
        for i2 in range(i1+1, n):
            if lst[i1] < lst[i2] : 
                lst[i1], lst[i2] = lst[i2], lst[i1]
    print(cnt, lst)

위의 예제는 bubble sort를 파이썬에서 실행하는 함수로, 데이터 구조는 list를 사용하여 nested for loop 구문을 통해 list 안의 숫자들을 크기 순서로 재배열해줍니다. bubble sort의 실행 횟수를 세주는 것이 쉽지 않은 이유는 if 구문이 포함되어 있기 때문입니다. 예를 들어, 운이 좋게 [3, 2, 1]을 입력받았다면 위의 알고리즘은 if 구문 안의 내용을 실행시킬 필요가 없게 됩니다. 반면에 [1, 2, 3]과 같이 입력받아다면 모든 반복마다 if 구문을 실행해주게 됩니다. 즉 데이터의 크기 N이 동일하더라도 그 값이 달라지게 되는 것입니다.

그렇기 때문에 우리는 다양한 시간복잡도를 구할 수 있게 됩니다. 실제로 다양한 실행횟수들의 평균 (평균 시간복잡도, average-case analysis)를 구하기도 하고, 가장 오래 걸리는 경우를 기준으로 잡는 worst-case analysis를 사용하기도 합니다.

Asymptotic notation

asymptotic notation(점근 표기법)은 시간복잡도를 간단하게 표현하는 표기법입니다. 당연히 시간복잡도가 다양했던 것처럼, 점근 표기법도 다양합니다. 예를 들어 최선의 경우에 해당하는 시간복잡도는 간편하게 $\Omega$(빅-오메가)로 표기하고, 최악의 경우는 $O$(빅-오)로, 평균은 $\theta$(빅-세타) 표기하는 식입니다.

Big O notation

다양한 기준과 그에 맞는 표기법이 있지만, 산업에서 가장 일상적으로 쓰이는 것은 big O입니다. 대다수 최악의 경우에 더 민감할 뿐아니라, 상대적으로 간단하게 구할 수 있기 때문입니다. 따라서 이를 기준으로 polynomial time 등을 논하게 됩니다. 그리고 사실 중요한 이야기는 polynomial time과 이를 바탕으로 하는 P and NP 문제이기도 합니다. 이는 잠시 뒤에 다루도록 하겠습니다.

앞에서 사용했던 두 예제를 다시 살펴보겠습니다. 누적합을 구해주는 알고리즘의 최악 시행횟수는 총 2n+2였습니다. 이 경우에 우리는 $O(n)$으로 표현합니다.¹ 버블 정렬의 최악 시행횟수는 ${3\over2}n^2 - {1\over2}n+1$에 해당합니다.² 이 경우에 더욱 간편하게 빅O 표기법을 활용해서 $O(n^2)$으로 표현합니다.

어떻게 했길래, 2n+2는 $O(n)$으로, ${3\over2}n^2 - {1\over2}n+1$는 $O(n^2)$으로 바꿔서 표현할 수 있는지는 Big O notation의 수학적 정의를 바탕으로 설명할 수 있습니다. 예를 들어 $f(N)$이라 함수를 빅O 노테이션을 사용해서 $O(g(N))$꼴로 바꾸고 싶다면 이는 아래와 같은 가정을 만족하고 있을 때에만 가능합니다.

There are positive constants $c$ and $n_0$ s.t. $f(N) \leq cg(N)$ when $N \geq n_0$

위의 정의식은 매우 간결하고 분명하긴 하지만 조금 더 친숙하게 풀어서 설명하면 다음과 비슷합니다.

상수 $c$를 곱해줘서 $g(n)$의 값을 키워주는 한이 있어도, 특정한 값($n_0$) 이상부터는 항상 $g(n)$이 커야한다.

따라서 만약 $f(n)$이 $n^2$이라면 $g(n)$으로 가능한 값은 반드시 이차항 이상의 값이어야 합니다. 예를 들어 $g(n)$이 $n$이라면 아무리 큰 상수 $c$를 곱해줘도 $n$이 어느 정도 커지면 제곱으로 증가하는 $f(n)$의 성장률을 이길 수 없게 되기 때문입니다. 결국 $f(n)$이 다항식이라면, 항상 $g(n)$은 다항식의 최고차항 또는 그 항보다 높은 차수의 항이 되게 됩니다.³ 따라서 빅O 노테이션으로 표현한 시간복잡도에서 가장 중요한 것은 반복문이 되게 됩니다. 반복문이 아닌 실행명령은 상수항으로 취급되어서 생략되기 때문입니다. 위의 두 예시에서도 이를 확인할 수 있습니다.

덧붙여, 앞서서 다항식의 $g(n)$은 최고차항보다 높은 차수도 성립함을 이해했습니다. 예를 들어 $f(n)$이 $n^2$이라면 $g(n)$은 2차항보다 큰 차수인, $n^3$, $n^4$ 등도 모두 성립이 가능합니다. 이럴 때 만약 $g(n)$을 최고차항으로 쓴다는 것을 일컬어 tight하게 잡아주었다 고 표현합니다.⁴ 사실 이미 worst-case 분석이기 때문에 굳이 더 높은 차수를 사용해서 over-estimate할 필요는 없기 때문에 이를 best answer로 취급합니다.

growth rate

위에서 빅O 노테이션을 알아봤습니다. 빅O 노테이션은 결국, $f(n)$의 성장률보다 크거나 같은 $g(n)$으로 함수를 간단하게 표현하는 것을 뜻합니다. 이렇게 되면, 우리는 알고리즘이 데이터 크기 $n$에 따라서 최악의 경우 처리하게 될 시행횟수가 얼만큼 비례적으로 증가하게 되는지를 간편하게 비교할 수 있게 됩니다. 아래의 사진은 대표적인 빅O 노테이션을 보여줍니다.

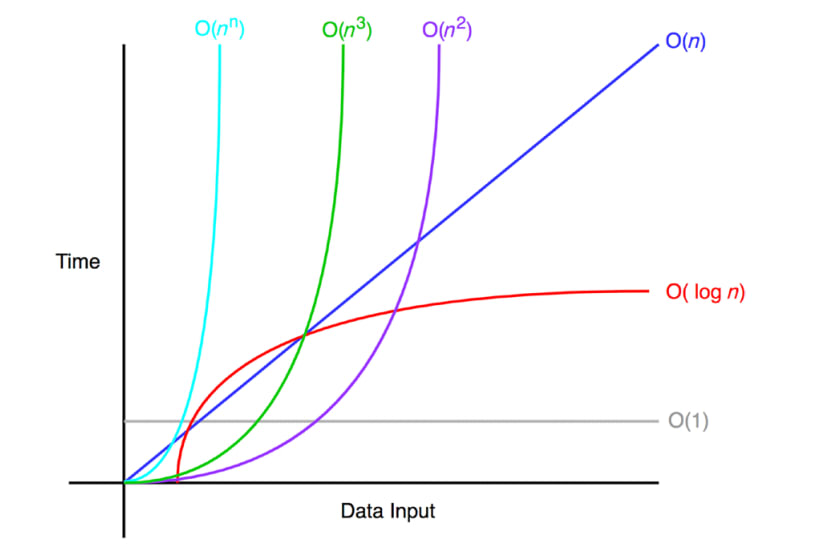
마지막으로 몇 가지 빅O 노테이션의 성질을 짚고 넘어가려고 합니다. 빅O 노테이션을 통해서 함수의 성장률을 감안해준다는 것은, 이보다 낮은 항과 최고차항의 계수를 완전히 무시해준다는 것을 뜻합니다. 이는 앞에 정의에서 $g(n)$에 $c$를 어차피 곱해준다고 했기 때문에 최고차항만 고려해주어도 손쉽게 $f(n)$ 값보다 커지도록 조정해줄 수 있기 때문입니다. 이러한 관점에서 $log$의 밑(base)도 적어주지 않아도 무방하게 됩니다. 조금 까다로운 특색은 아래와 같은 성질들입니다.

1. If $T_1(N) = O(f(N))$ and $T_2(N) = O(g(N))$, then $T_1(N)+T_2(N)=max(O(f(N)), O(g(N)))$
2. $T_1(N) * T_2(N) = O(f(N)) * O(g(N))$.

새로운 표기법 $T_i$는 $i$번째 알고리즘을 실행할 때 필요한 연산 횟수라고 보면 됩니다. 따라서 위의 성질은 두 알고리즘을 동시에 사용할 때는 더하기를 통해서, 함수 안에서 다른 함수를 call하는 경우는 곱하기로 나타낸다는 것을 의미합니다. 예를 들어 N 길이를 가지는 리스트를 binary search tree에 집어넣는 경우를 떠올리면 후자를 쉽게 이해하실 수 있을 겁니다.⁵ 이러한 식으로 알고리즘의 complexity를 손쉽게 확장해나갈 수 있게됩니다.

polynomial time

위의 성장률을 보여주는 사진에서도 볼 수 있듯이, $g(n)$이 다항식인지 지수함수인지에 따라서 n이 커질수록 엄청난 차이가 존재한다는 것을 알 수 있습니다.

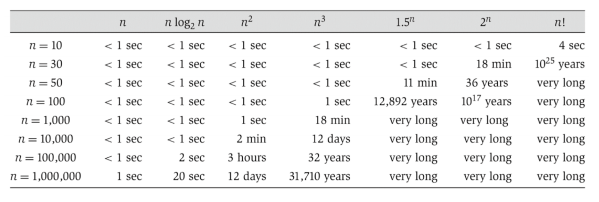
우리는 이 빅O 노테이션 안의 함수가 다항식을 뛸 때 알고리즘이 효율적이라고 이야기합니다. 즉 input 크기가 늘어나는 것에 대해 실행횟수가 polynomial scale로 증가하는 알고리즘이 좋은 알고리즘이 되는 것이죠. 그리고 이들을 가리켜 polynomial time algorithm이라고 말합니다. 앞에서 설명드렸던 버블정렬 또한 $O(n^2)$이였으므로 polynomial time algorithm이라고 할 수 있으며 따라서 효율적인 알고리즘의 한 예시가 됩니다.

사실 버블정렬이 좋은 알고리즘이라는게 잘 안 와닿을 수 있습니다. 파이썬을 자주 쓰시는 분들이라면 for 구문을 nested loop로 쓰는 것이 얼만큼 느린지 경험해보신 적들이 있으실 겁니다. 그럴 때는 exponential time이 소요되는 알고리즘과 비교해보면 polynomial time algorithm이 얼마나 좋은 것인지 확인할 수 있습니다.

예컨데 $O(10^n)$인 알고리즘과 버블 정렬을 비교해보겠습니다. 정렬해야하는 input size가 50, 100, 150으로 증가해진다면 전자의 알고리즘은 최악의 경우 각각 $10^{50}, 10^{100}, 10^{150}$의 시행횟수가 필요하지만 버블정렬은 단 2,500, 10,000, 22,500번뿐입니다. 데이터가 3배 증가했을 뿐인데 두 알고리즘의 성능차이는 도저히 비교할 수 없게 되는 것입니다.

이처럼 exponential algorithm은 실제로 쓸 수 없는 알고리즘으로 취급하는만큼, polynomial time algorithm을 개발하는 것은 매우 중요합니다. 실제로 세상에 많은 문제들은 못 푸는 경우가 아니라 아직 다항시간 알고리즘으로 개발이 되지 않은 경우인 상황이 많다고 합니다. 이와 관련해서는 P-NP 문제와 관련한 다음 포스팅에서 좀 더 자세히 알아보도록 하겠습니다.

각주 및 추천자료

추천자료

1. 시간복잡도 한국어 자료

각주